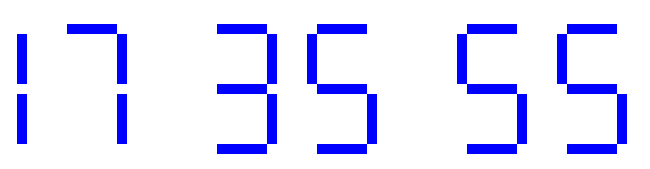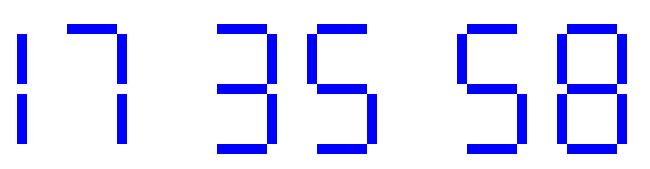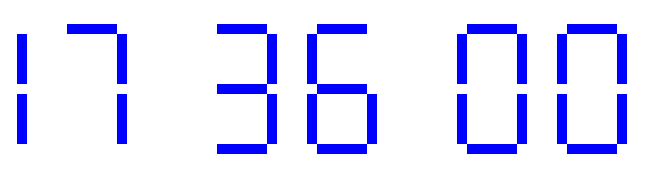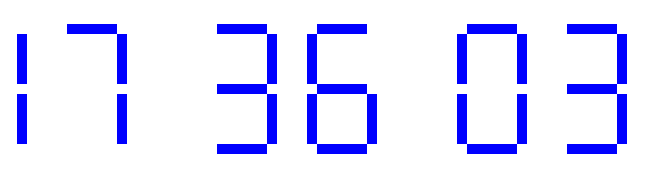EINLEITUNG

Siebensegmentanzeigen sind auch heute noch wegen ihrer Einfachheit und guten Lesbarkeit weit verbreitet. Sie bestehen aus 7 länglichen Leuchtquellen,  Segmente genannt, die gewöhnlich aus Leuchtdioden (LEDs) bestehen. Die Form der  Segmente kann leicht variieren, z.B. können die Segment geneigt oder an den Enden schräg abgeschnitten sein. Oft haben 7-Segmentanzeigen auch noch zusätzliche kleine LEDs, die als Dezimalpunkte oder Doppelpunkte. verwendet werden. Einzelne Displays werden hintereinander zu einem 7-Segment-Array angeordnet.

AUFGABENSTELLUNG UND ZIELSETZUNG

7-Segmentanzeigen werden auch oft auf Computerbildschirmen zur Anzeige von Daten und Messwerten, insbesondere für virtuelle Messinstrumente verwendet, da sie leicht lesbar sind. Darum soll in dieser Projektarbeit ein 7-Segment-Array mit einer beliebig wählbaren Zahl von Einzeldisplays softwaremässig modelliert werden.

Der Programmcode soll sich in verschiedenen Anwendungen einsetzen lassen, beispielsweise zur digitalen Anzeige der aktuellen Uhrzeit in Stunden, Minuten und Sekunden. Dabei wird Python als Programmiersprache und die TigerJython-Turtlegrafik als Grafiksystem verwendet. Standardmässig werden die Segmente mit den Buchstaben A bis G oder mit den Zahlen 0 bis 6 identifiziert. Wir verwenden hier die Nummerierung, da sie der Datenstruktur von Listen und Tupels besser angepasst ist. Es wird die im nebenstehenden Bild ersichtliche Nummerierung verwendet:

AUFGABE 1

7-Segmentanzeigen werden auch oft auf Computerbildschirmen zur Anzeige von Daten und Messwerten, insbesondere für virtuelle Messinstrumente verwendet, da sie leicht lesbar sind. Darum soll in dieser Projektarbeit ein 7-Segment-Array mit einer beliebig wählbaren Zahl von Einzeldisplays softwaremässig modelliert werden.

VORBEREITUNG ZUR AUFGABE 1

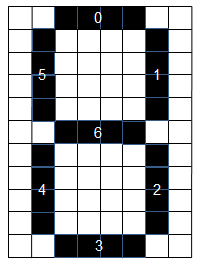
Das in der Abbildung gezeigte Raster stellt quadratische Zellen mit der Seitenlänge s dar, die als Konstante gewählt werden kann. Typisch ist s = 10 (in Turtlekoordinaten).

Die Informationen über die Lage und Ausrichtung der Segmente wird ein einer Liste gespeichert. Die Listenstruktur kann eher "flach" oder stark strukturiert sein. Wir wählen die flache Variante und speichern jedes Segment in 3 Zahlen x, y, heading, wo x,y die Koordinaten des Startpunkts und heading die Bewegungsrichtung der Turtle  (0 oder 90 Grad) sind. Das folgende Programmskelett zeigt dies für die Segmente 0 bis 3 und als Test werden diese Segmente der Reihe nach gezeigt.

from gturtle import *

s = 10 

def drawSegment(i):
    setPos(segments[3*i], segments[3*i + 1])
    heading(segments[3*i + 2])
    forward(4*s)

segments = [2*s, 12*s, 90, 7*s, 7*s, 0, 7*s, s, 0] 
            
makeTurtle()
hideTurtle()
setPenWidth(s)
for p in range(3):
   drawSegment(p)
   delay(1000)

Ergänze das Skelett, dass alle Segmente durchlaufen werden.

AUFGABE 2

Es ist deine Aufgabe, die Funktion drawNum(n) zu schreiben, die für den Parameter n = 0..9 die entsprechende Ziffer anzeigt, d.h. die richtigen Segmente zeichnet.

VORBEREITUNG ZUR AUFGABE 2

Die Information, welche Segmente bei einer bestimmten Zahl n = 0..9 leuchten, wird in der Liste patterns als Tupel  der Nummern der angezeigten Segmente gespeichert. Wie du leicht nachprüfen kannst, lauten die Tupel für die Zahlen 0..3 wie folgt:

patterns =  [(0, 1, 2, 3, 4, 5), (1, 2), (0, 1, 6, 4, 3, 4), (0, 1, 6, 2, 3)] Es ist deine Aufgabe, das folgende Skelett so zu ergänzen, dass die auskommentierten Zeilen die Ziffern 0..9 ausschreiben. Beachte, dass du in der Wiederholschleife mit clear() die Ziffern immer wieder löschen musst.

from gturtle import *

s = 10 

def drawSegment(i):
    setPos(segments[3*i], segments[3*i + 1])
    heading(segments[3*i + 2])
    forward(4*s)

def drawNum(n):
    pattern = patterns[n]
    for segment in pattern:
        drawSegment(segment)
        
segments = [2*s, 12*s, 90, 7*s, 7*s, 0, 7*s, s, 0]  

patterns =  [(0, 1, 2, 3, 4, 5), (1, 2), 
             (0, 1, 6, 4, 3, 4), (0, 1, 6, 2, 3)] 

makeTurtle()
hideTurtle()
setLineWidth(s)

drawNum(1)
#for n in range(10):
#    clear()
#    drawNum(n)
#    delay(1000)

AUFGABE 3

VORBEREITUNG ZUR AUFGABE 3

Um für Zahlen > 10 die beiden Ziffern zu bestimmen, verwendest du für die Einer den Modulo-Operator % und für die Zehner die Ganzzahldivision mit dem verdoppelten Bruchstrich //. Die Zählschleife lautet:

for n in range(100):
    clear()
    if n < 10:
        drawNum(0, 0)
        drawNum(n, 100)
    else:
        drawNum(n // 10, 0)
        drawNum(n % 10, 100)
    delay(1000)

AUFGABE 4

VORBEREITUNG ZUR AUFGABE 3

Wenn du import time verwendest, so kannst du Stunden, Minuten und Sekunden mit folgender Funktion als Strings im Format hhmmss erhalten:

t = time.strftime("%H%M%S")

Die Ziffern als Zahlen musst du dann mit int(t[0]), int(t[1]), ..,int(t[5]) extrahieren. Du solltest aus Effizienzgründen die Wiederholschleife nur ungefähr alle 50 ms durchlaufen, da ja die Anzeige sowieso nur alle Sekunden ändert. Auch so kann das Bild flackern, da es sich ja um eine Computeranimation handelt. Wie du in der entsprechenden Lektion gelernt hast, solltest du daher mit enableRepaint(False) die Doppelbufferung einschalten und die Anzeige mit repaint() auf dem Bildschirm rendern.

VERBESSERNGSVORSCHLÄGE/ERWEITERUNGEN