OBJECTIFS DE CETTE SECTION...

STRUCTURE SÉQUENTIELLE D'UN PROGRAMME

Un programme informatique est constitué de plusieurs lignes de code organisée séquentiellement qui vont s’exécuter les unes après les autres. Pour pouvoir utiliser la luciole, il faut toujours commencer le programme par la ligne

from mbglow import *

permettant de charger le module mbutils.

Dès que ce module a été importé, une luciole rouge apparaît au milieu de l’écran du micro:bit. Il s’agit d’une unique LED de l’écran qui a été allumée. Lors de l’utilisation des instructions de mouvement, d’autres LEDs de l’écran s’allument. La luciole laisse donc une trace derrière elle. Les instructions sont automatiquement exécutées par le micro:bit dès que le code a été téléchargé dessus.

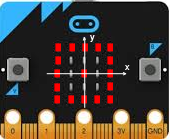
Les instructions de la luciole sont essentiellement des mots anglais suivis de parenthèses qui peuvent contenir d’autres expressions. Il est essentiel de respecter la casse (faire la différence entre les majuscules et les minuscules).

L’instruction forward()demande à la luciole de se déplacer d’un pas en avant par rapport à la direction dans laquelle elle regarde. Au début de l’exécution du programme, la luciole regarde toujours vers le haut. Il est possible de tourner la luciole de 90° vers la gauche avec la commande left(90)et de 90° vers la droite avec la commande right(90) On ne remarque cependant rien tant que la luciole n’a pas avancé avec forward() .

Le programme suivant demande à la luciole de dessiner la trace représentée :

Program: from mbglow import * makeGlow() forward() left(90) forward() right(90) forward() from mbglow import * makeGlow() forward() left(90) forward() right(90) forward() ► Copy to clipboard

Il est conseillé de recopier ce programme dans l’éditeur de TigerJython ou de faire du copier-coller afin de le tester. Pour le copier, il faut cliquer sur Copy to clipboard et le coller dans l’éditeur de TigerJython avec Ctrl+V.

RÉPÉTITION AVEC REPEAT

Pour effectuer une trace carrée, la luciole doit effectuer 4 fois de suite les instructions forward() et left (90) . On peut économiser de nombreuses lignes de code en utilisant une boucle de répétition au lieu de copier ces deux instructions plusieurs fois d’affilée. Pour ce faire, il suffit d’écrire repeat 4: (le double-point est capital). Les instructions qui doivent être répétées au sein de la boucle doivent être indentées de manière identique par rapport à l’instruction  repeat , par exemple une tabulation ou 4 espaces.

Program:

from mbglow import *

makeGlow()

repeat 4:
    forward()
    left(90)

INFORMATION DIDACTIQUE

Le mot-clé repeat ne fait pas partie de la syntaxe conventionnelle de Python mais a été défini dans TigerJython pour permettre l’introduction très précoce des boucles, sans même avoir besoin de parler de variables. De telles structures de répétition sont très naturelles car on parle très souvent de répéter une tâche un certain nombre de fois dans la vie courante.

Si l’on veut rester compatible avec le langage Python standard, il faut remplacer les instructions repeat n: par for step in range(n):.

On peut fabriquer des boucles infinies en laissant tomber le nombre n de l’instruction, à savoir en écrivant simplement repeat.

Pour dessiner le plus grand carré possible, on commence par placer la luciole au coin inférieur gauche avec setPos(-2, -2) Il est donc possible de déplacer la luciole sans faire de trace avec l’instruction setPos(x, y). Les paramètres x et y prennent les valeurs entières -2, -1, 0, 1 ou 2. Pour dessiner les côtés du carré, il faut donc déplacer la tortue 4 fois vers l’avant, ce qui peut également s’exprimer avec une boucle repeat.

Attention ! Il faut être très attentif à l’indentation des lignes au sein des boucles repeat.

Program:

from mbglow import *

makeGlow()

setPos(-2, -2)
repeat 4:
    repeat 4:
        forward()
    right(90)

FONCTIONS (BLOCS DE CODE NOMMÉS)

Les blocs de code nommés, appelés fonctions en Python, permettent de mieux organiser les programmes et de les rendre plus clairs et plus lisibles. Il est possible d’appeler à plusieurs reprises des fonctions personnalisées. L’utilisation des fonctions est essentielle pour éviter de devoir copier-coller à différents endroits du code des instructions identiques ou très similaires (duplication de code) et elles rendent également possible de décomposer les problèmes en sous-problèmes plus facilement résolubles.

Dans l’exemple suivant, on définit une fonction square() qui déplace la luciole sur un carré. La définition de la fonctiondébute avec le mot-clé def. uivi du nom de la fonction, d’une liste de paramètres entre parenthèses et finalement un double-point (:). La fonction ainsi définie est exécutée lors de l'appel de function. Dans tous les cas, il faut que la définition de la fonction précède un quelconque appel.

Il est important, pour une bonne lisibilité du programme, de baptiser la fonction d’un nom descriptif qui renseigne sur ce que la fonction fait. Il n’est pas autorisé d’utiliser des caractères spéciaux pour nommer les fonctions (espaces, guillemets simples ou doubles, accents, caractères de ponctuation, etc ...). La convention veut que les noms de fonctions débutent toujours par une minuscule.

Program:

from mbglow import *

makeGlow()

def square():
    repeat 4:
        forward()
        forward()
        left(90)

square()

Il est possible d’appeler une fonction plusieurs fois d’affilée. Par exemple, pour dessiner la figure ci-contre, on appelle la fonction L’instruction setSpeed(80) permet d’accélérer les déplacements de la tortue. La valeur par défaut est 50 et les valeurs autorisées sont entre 0 et 100.

Program:

from mbglow import *

makeGlow()

def square():
    repeat 4:
        forward()
        forward()
        left(90)

setSpeed(80)
repeat 4:
    square()
    right(90)

VARIABLES

En informatique, les variables permettent de stocker des valeurs qui changent durant l’exécution du programme. Une variable possède donc un nom et une valeur. Le programme ci-dessous utilise une variable v qui contient initialement la valeur 30 (v = 30) et correspond à la vitesse de la luciole. Cette vitesse augmente de 20 à chaque fois qu’elle commence à dessiner un nouveau carré.

La ligne v = v + 20qui, au premier coup d’œil, ressemble à s’y méprendre à une équation va en réalité changer la valeur contenue dans la variable v en ajoutant 20 à la valeur actuellement stockée dans v et en affectant ce nouveau résultat à la variable v. Il s’agit d’une affectation. L’instruction showTrace(False) a pour conséquence que la luciole ne laisse pas de trace derrière elle.

Program:

from mbglow import *

makeGlow()

def square():
    repeat 4:
        forward()
        forward()
        right(90)
    
v = 30
showTrace(False)
setPos(-1, -1)

repeat 4:
    setSpeed(v)
    square()
    v = v + 20

RÉPÉTITION AVEC UNE BOUCLE WHILE

La boucle while compte parmi les structures de programmation les plus importantes. Elle peut être utilisée dans toutes les circonstances où il faut répéter un bloc de code et on la retrouve dans pratiquement tous les langages de programmation. Cette structure de contrôle est introduite par le mot-clé while suivi d’une expression booléenne (conditionnelle) et du double-point habituel. Tant que la condition en question vraie, les instructions contenues dans le bloc de code indenté sont répétées. En langage courant, on pourrait exprimer cette structure de la manière suivante :

TANT QUE la condition est vraie: Exécuter les instructions

L’expression conditionnelle (booléenne) utilise en général des opérateurs de comparaison tels que

• < Plus petit que
• <= Plus petit ou égal
• > Plus grand que
• >= Plus grand ou égal
• == Égal
• != Pas égal

Remarquez qu’il y a deux égal d’affilée pour signifier l’opérateur qui compare l’égalité.

Dans l’exemple suivant, la luciole se déplace d’abord de deux pas en avant puis deux pas en arrière, se tourne de 45° vers la gauche, recommence à avancer de deux pas et ainsi de suite jusqu’à ce qu’elle pointe à nouveau vers le Nord. La variable a permet d’enregistrer la somme des angles dont la luciole a tourné. La variable a possède donc initialement la valeur 0, augmente cette valeur de 45° à chaque parcours de la boucle while, jusqu’à ce que la valeur contenue dans a soit 360°.

Program:

from mbglow import *

makeGlow()

setSpeed(90)
showTrace(False)
a = 0
while a <= 360:
    forward()
    forward()
    back()
    back()
    left(45)    
    a = a + 45

La boucle while revêt une importance toute particulière pour la programmation du micro:bit car, en robotique, on utilise souvent une boucle while infinie. Une boucle while est infinie si la condition qui contrôle l’exécution de la boucle est toujours évaluée à une valeur vraie. Le plus simple pour créer une telle boucle infinie est d’écrire while True: Comme la valeur True est par définition toujours vraie, la boucle va tourner tant que le programme n’est pas interrompu depuis TigerJython (Ctrl+C) ou par une réinitialisation du micro:bit. La fonction clear()permet de réinitialiser toutes les LEDs de l’écran.

Program:

from mbglow  import *

makeGlow()

def square():
    repeat 4:
        forward()
        forward()
        left(90)

clear()
setSpeed(90)
showTrace(False)
setPos(2, 0)
left(45)
while True:
    square()

RÉPÉTITION AVEC LA STRUCTURE FOR IN RANGE

Souvent, on utiliser une variable entière qui va être incrémentée (augmentée de 1) lors de chaque itération (=passage) de la boucle. Il est bien entendu possible de réaliser un tel scénario avec une boucle while en écrivant. i = 0 while i < N: # do something with variable i i = i + 1

Il est cependant bien plus pratique d’utiliser une boucle for dans ce cas car la variable i va être gérée incrémentée automatiquement, ce qui élimine des sources d’erreur.

Avec la boucle for i in range(n):, la variable i prend successivement des valeurs entières comprises entre 0 et n-1 alors qu’avec la boucle for i in range(a, b), elle va prendre toutes les valeurs entières entre a et b - 1. Il faut remarquer que la dernière valeur (n, respectivement b) ne sont jamais incluses.

Avec la boucle for x in range(-2, 3), la variable x va donc prendre les valeurs -2, -1, 0, 1, 2. Cela va enclencher successivement les LEDS de la première rangée les unes après les autres. L’instruction sleep(500)permet quant à elle de mettre le programme en pause pendant 500 ms, ce qui permet à la rétine de constater l’avancement de la luciole.

Program:

from mbglow import *

makeGlow()

clear()
for x in range(-2, 3):
    setPos(x, 2)
    sleep(500)

Des boucles imbriquées sont souvent utilisées, par exemple, si vous souhaitez allumer les voyants une rangée à la fois. Tout d'abord, la ligne la plus basse est sur -2, puis avec y = -1 la deuxième ligne la plus basse, etc.

Program:

from mbglow  import *

makeGlow()

clear()
for y in range(-2, 3):
    for x in range(-2, 3):
        setPos(x, y)
        sleep(300)

STRUCTURE IF - ELSE (SÉLECTION)

La structure de sélection permet de faire en sorte que certains blocs de code ne s’exécutent que sous certaines conditions. Une telle structure est introduite par le mot-clé if suivi d’une condition. Si la condition est vraie, c’est le bloc d’instruction sous le if else qui le sera. Pour exprimer la condition, on utilise très souvent les opérateurs de comparaison <, <=, =>, >, == et !=. Les instructions sous le if et le else doivent être indentées de manière cohérente. La partie else est optionnelle.

Dans l’exemple suivant, la luciole se déplace vers la droite. Dès qu’elle arrive au bord droit, elle repart du bord gauche et répète ce mouvement à l’infini. On déplace donc la luciole avec forward() et on teste, à chaque pas, sa coordonnée x. Si cette coordonnée vaut 3, on replace la luciole au bord gauche (x = -2).

Program:

from mbglow import *

makeGlow()

right(90)
x = 0
showTrace(False) 

while True:
    forward()
    x = x + 1  
    if x == 3:
        setPos(-2, 0)        
        x = -2 

Dans le programme suivant, la luciole doit aléatoirement faire deux pas en avant ou en arrière, marquer une courte pause et effacer sa trace et regagner sa position de départ. Ce mouvement est répété 20 fois de suite.

Pour réaliser ce programme, il est nécessaire d’utiliser des nombres aléatoires. La fonction randint(a, b) génère un nombre pseudo-aléatoire compris entre a et b. De ce fait, l’appel randint(0, 1) génère un nombre entier entre 0 et 1, à savoir soit un 0, soit un 1. Si le nombre généré vaut 1, on décide que la luciole avance de deux pas, sinon (lorsque le nombre généré est 0), elle fait deux pas en arrière.

Program:

from mbglow import *
from random import randint

makeGlow()
setSpeed(80)
repeat 10:    
    r = randint(0, 1)
    if r == 1:
        forward()
        forward()
    else:
        back()
        back()     
    sleep(300)
    clear()
    setPos(0, 0) 

À RETENIR

Les structures de programmation fondamentales à maîtriser au minimum pour pouvoir programmer sont suivantes :

• Une séquence d’instructions exécute les instructions les unes après les autres de manière linéaire.
• Les répétitions permettent de répéter plusieurs fois l’exécution d’un bloc de code. TigerJython met à disposition les boucles repeat, for et while pour créer des répétitions.
• La sélection if ****/ else ****fait en sorte que les instructions concernées ne s’exécutent que sous certaines conditions. La partie else ****est facultative.

À TOI DE JOUER