while&for

10. WHILE & FOR

 

 

DU LERNST HIER...

 

wie du die Wiederholstrukturen mit den Keywords while und for verwendest. Es handelt sich um die wichtigsten Programmstrukturen überhaupt. Sie sind allgemeiner anwendbar ale die repeat-Schleife, die du bereits kennst.

 

 

MUSTERBEISPIELE ZUR WHILE-SCHLEIFE

 

Umgangssprachlich kann die while-Schleife so formuliert werden: "Solange die folgende Bedingung erfüllt ist, führe den nachfolgenden Programmblock aus..." Um die Bedingung zu definieren brauchst du eine Schleifenvariable, die einen Startwert erhält (hier a = 1). Nach while folgt die Bedingung und ein Doppelpunkt. Der nachfolgende Programmblock muss eingerückt sein.
Der Wert der Variablen a wird nach jedem Schleifendurchlauf um 5 grösser. 

from gturtle import *

makeTurtle()
hideTurtle()

a = 1
while a < 500:
    forward(a)
    right(90)
    a =  a + 5
► In Zwischenablage kopieren 		 

Die while-Schleife wird insbesondere dann verwendet, wenn die Anzahl der Wiederholungen im voraus nicht bekannst ist oder wenn die Schleifenvariable nicht nur ganze Zahlen durchläuft. In diesem Beispiel ändert der Drehwinkel mit dem Faktor 1.01 und lässt eine interessante Grafik entstehen.

from gturtle import *

makeTurtle()
hideTurtle()
setPos(-300, -200)

a = 1
while a < 100:
    forward(8)
    right(a)
    a =  a * 1.01
► In Zwischenablage kopieren 		 

 

 

MERKE DIR...
 

Der Schleifenvariablen a wird zuerst ein Startwert zugewiesen. Die Bedingung nach while nennt man auch Laufbedingung, da sie wahr sein muss, damit der Block durchlaufen wird. Der Wert der Schleifenvariablen wird nach jedem Schleifendurchlauf verändert.

 

 

ZUM SELBST LÖSEN


  1.

Die Turtle zeichnet eine 6-Eck-förmige Figur. Die erste Strecke ist 100, jede nächste Strecke ist um 2 kürzer, solange die Streckenlänge grösser als 5 ist.

  
  2.

Die Turtle bewegt sich a = 10 Schritte vorwärts, zeichnet einen Punkt, bewegt sich um die gleiche Strecke zurück und dreht 10 Grad nach rechts. Dann vergrössert sie die Streckenlänge a um 10. Diese Bewegung wierderholt sie so lange die Streckenlänge a kleiner als 300 ist

  
  3.

Die Turtle soll wiederholt 100 Schritte vorwärts gehen und 122 Grad links drehen. Nach 30 Sekunden soll sie sich zur Ruhe setzen.

Anleitung: Mit time.time() liefert dir das System die aktuelle Uhrzeit in Sekunden. Dazu musst du mit import time das Modul time importieren. Willst du ein Zeitintervall bestimmen, so musst du die Anfangszeit in einer Variablen startTime speichern und die Differenz time.time() - startTime bilden.

 

 

 

MUSTERBEISPIELE ZUR FOR-SCHLEIFE
  Für Aufgaben mit ganzahligen Schleifenvariablen kann anstelle einer while-Schleife eine for-Schleife verwendet werden. Die Schleifedefinition benötigt nur eine Programmzeile.

Die einfachste for-Schleife hat die Form:

for i in range(n):
      (Schleifenkörper)

Die Schleifenvariable i durchläuft die Zahlen von 0 bis n-1, also n Zahlen. In diesem Beispiel verwendest du die Variable i zudem für das Zeichnen der Grafik.

Mit der Funktion line(x1, y1, x2, y2) zeichnet eine Linie vom Punkt (x1, y1) zum Punkt (x2, y2). Nachfolgend zeichnest du damit eine Linienschar. delay(100) bewirkt nach jeder gezeichneten Linie ein kurze Pause.

   



from gturtle import *

def line(x1, y1, x2, y2):
    setPos(x1, y1)
    moveTo(x2, y2)
    
makeTurtle()
hideTurtle()

for i in range(31):
    line(10 * i, 0, 300, 10 * i)
    delay(100)
► In Zwischenablage kopieren


Die allgemeine Form einer for-Schleife hat 3 Parameter :
for i in range(start, stop, step):
Zuerst ist i = start. So lange i kleiner ist als stop, wird die Schleife wiederholt, wobei i bei jedem Durchgang um step vergrössert wird. Hier verwendest du eine for-Schleife, um die Koordinaten der Punkte festzulegen.

for i in range(-240, 250, 20):

Der erste Punkt hat die Koordinaten (-240, -240), der zweite (-220, -220).... der letze (240, 240).		   


from gturtle import *

makeTurtle()

for i in range(-240, 250 , 20):    
    setPos(i, i)
    dot(15)
► In Zwischenablage kopieren

Du kannst die Aufgabe auch mit einer repeat-Schleife lösen. Allerdings musst du vorher ausrechnen, wie viele Punkte du zeichnen musst.

from gturtle import *

makeTurtle()

i = -240
repeat 25:   
    setPos(i, i)
    dot(15)
    i = i + 20

 

 

GESCHACHTELTE FOR-SCHLEIFEN
 

Die for-Schleifen lassen sich einfach "verschachteln". In diesem Beispiel durchläufst du mit step = 20 die (x, y) - Koordinaten im Bereich -200, 200. Damit auch 200 berücksichtigt wird, ist der zweite Parameter 201.

from gturtle import *

makeTurtle()

for x in range(-200, 201, 20):
    for y in range(-200, 201, 20):   
        if x + y > 0:
            setPenColor("red")
        else:
            setPenColor("blue")
        setPos(x, y)
        dot(10)
► In Zwischenablage kopieren 		 

Im nächsten Beispiel zeichnest du ein Schachbrett. Das Gitter mit 8 horizontalen und 8 vertikalen Zellen kannst du mit Hilfe von zwei geschachtelten for-Schleifen durchlaufen (i sind Zeilen, k sind Spalten). Ein Feld hat die Grösse 30x30. Es werden nur Felder gezeichnet, für welche die Summe i + k eine gerade Zahl ist.
Das Feld (i, k) zeichnest du an der Position x = 30 * i, y = k * 30.

   

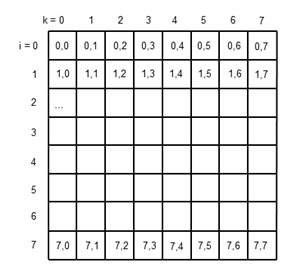
from gturtle import *

def field(x, y):
    setPos(x, y)
    startPath()
    repeat 4:
        forward(30)
        left(90)
    fillPath()    

makeTurtle()
hideTurtle()
for i in range(8):
    for k in range(8):
        if (i + k) % 2 == 0:
            field(30 * i, 30 * k)
► In Zwischenablage kopieren

 

 

MERKE DIR...
  for i in range(20): durchläuft die Zahlen 0, 1, 2,..19.
Eine for-Schleife kann auch 2 oder 3 Parameter haben.
for i in range(5, 20): durchläuft die Zahlen 5, 6, 7, 8.....19. (step = 1).
for i in range(5, 20, 3): durchläuft die Zahlen 5, 8, 11, 14, 17.

 

 

ZUM SELBST LÖSEN

  4.

Mit dem Befehl openDot(d) erzeugst du 20 Kreise wobei du die Turtle nach jedem gezeichneten Kreis 5 Schritte vorwärts laufen lässt. Verwede den Befehl penUp() , damit die Turtle beim Vorrücken keine Spur hinterlässt.

  

  5.

Orientiere dich am Beispiel zu geschachtelten for-Schleifen und zeichne das nebenstehende Muster. Die gefüllten Kreise haben hier den Durchmesser 30.

Löse die gleiche Aufgabe mit Hilfe von repeat-Schleifen.

  

  6.

Zeichne die nebenstehende Figur mit Hilfe von zwei for-Schleifen.

  

 

 

   

 

10-2
Fachliche Hinweise:

While-Schleifen sind dann interessant, wenn die Anzahl Durchläufe einer Wiederholschleife nicht zum vornherein feststeht. Umgekehrt kannst du jede Aufgabe, die du mit repeat lösen kannst, auch mit einer while-Schleife lösen:

Lösung mit repeat   Lösung mit while 
from gturtle import *

makeTurtle()
repeat 6:
    forward(80)
    right(60)
  
from gturtle import *

makeTurtle()
a = 0
while a < 6:
    forward(80)
    right(60)
    a = a + 1

 

10-3
Fachlicher Hinweis:

Anders als in der Mathematik ist a = a + 5 nicht eine Gleichung, sondern eine Zuweisung. Dem aktuellen Wert der Variablen a wird der Wert a + 5 zugewiesen.
Anstelle a = a + 5 kann kurz a += 5 geschrieben werden.

 

10-5
Fachliche Hinweise:

In der Informatik beginnt eine Aufzählung mittels eines Index immer mit 0, d.h. das erste Element hat den Index 0, das zweite den Index 1, usw. Dieser Unterschied zum täglichen Leben, wo man üblicherweise bei einer Zählung mit 1 beginnt.
Man merke sich:  n-Elemente haben immer die Indizes 0 bis n-1.

10-6
Fachlicher Hinweis:

Zeilen- und Spaltenindizes beim Zeichnen von Schachbrett